关联算法之-Apriori

发表于 更新于 分类于 本文字数： 2.1k 阅读时长 ≈ 8 分钟

简单介绍一下什么是Apriori算法： Apriori算法是一种挖掘关联规则的频繁项集算法，其核心思想是通过候选集生成和情节的向下封闭检测两个阶段来挖掘频繁项集。 Apriori（先验的，推测的）算法应用广泛，可用于消费市场价格分析，猜测顾客的消费习惯；网络安全领域中的入侵检测技术；可用在用于高校管理中，根据挖掘规则可以有效地辅助学校管理部门有针对性的开展贫困助学工作；也可用在移动通信领域中，指导运营商的业务运营和辅助业务提供商的决策制定。

背景知识

关联规则做数据挖掘一般的步骤可以分为两大类：

  1. 依据支持度找出所有频繁项集(频度)
  2. 依据置信度产生关联规则

基本概念

上面提到了两个概念：支持度和置信度。其实数据挖掘里面的概念很多，这里简单介绍几个最基本的术语，后面的变量和集合都会用到。

定义

  1. 资料库(transaction database):存储着二维结构的记录集，定义为D
    **备注:**这个可以理解为数据库里面的交易记录，每一条交易为一条记录，所有这些需要挖掘的数据构成了一个记录集。

  2. 所有项集(items):所有项目的集合，定义为I.
    **备注:**这个可以理解为，把资料库里的每一条记录拆分成最小单位，最后构成的一个集合

  3. 记录(transaction):在资料库的一笔记录。定义为T,T∈D

  4. 项集(itemset):同时出现项的集合。定义为：k-itemset(k项集)
    **备注:**同时出现项的集合意思是所有项集里面的单个项或者多个项组合成的一条记录
    解释:[[1, 3, 4], [2, 3, 5], [1, 2, 3, 5], [2, 5]]就是资料库D，里面有4条记录，所有项集I为[[1],[2],[3],[4],[5]],有5项；[1,3,4]为其中一条记录T;[2,5]称为2项集，[2,3,5]称为3项集。

  5. 支持度(support):定义为
    $supp(X)=\frac{occur(X)}{count(D)}=P(X)$.
    **备注:**支持度可以简单理解为投票，选举这种，在总人数(资料库),有多少人是选择支持你的，即X出现的次数(频度),即X出现的概率

  6. 置信度(confidence/strength):定义为
    $conf(X->Y)=\frac{supp(X∪Y)}{supp(X)}$
    即下面的意思$P(Y|X)=\frac{P(XY)}{P(X)}$
    **备注:**这个公式可以这么理解，买了X的人有多少人会同时会买Y，这就是X对Y的推荐度，概率论中的解释就是P(Y|X)=P(XY)/P(X)。看一个例子：
    例子：[支持度:3%,置信度:40%]
    支持度3%：意味着3%顾客同时购买牛奶和面包
    置信度40%：意味着购买牛奶的顾客40%也购买面包

  7. 候选集(Candidate itemset):通过合并得出的项集,有k个元素的候选集记为C[k].

  8. 频繁集(Frequent itemset):支持度>=特定的最小支持度(Minimum Support/minsup)的项集,表示为L[k].
    **注意:**频繁集的子集一定是频繁集,这个也好理解,假设子集都不满足最小支持度,那么与他组合的概率必然是只会比这个概率更小,参见概率论里面的联合概率.

  9. 提升比率(提升度Lift):
    $lift(X->Y)=lift(Y->X)
    =\frac{conf(X->Y)}{supp(Y)}=\frac{conf(Y->X)}{supp(X)}
    =\frac{P(XY)}{P(X)P(Y)}$
    经过关联规则分析后,针对某些人推销(根据某规则)比盲目推销(一般来说是整个数据)的比例,这个比率越高越好,我们称这个为强规则,这个可以理解为:假设买了X的人多半会买Y,那么我们就对买了X的人推销Y.

Apriori原理

Apriori例子

先来个简单的例子,最初这个例子来源于零售商,我们假设有4个商品,编号为0,1,2,3,那么能够被一起购买的商品组合为: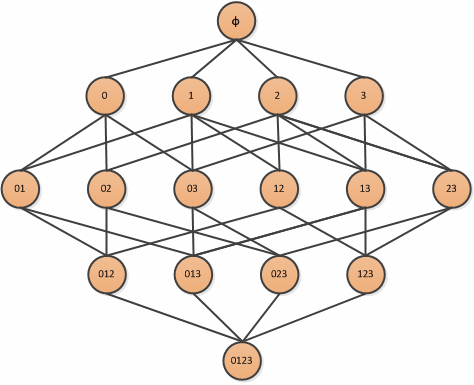
集合{0,1,2,3}中所有可能项集的组合
我们的目标是找到经常一起购买的商品,这里就可以使用集合的支持度来衡量一个组合出现的频率.即某个组合出现的概率占总交易量的比例就是其支持度.这个理解起来很简单,但是计算起来计算量可不小,这里才4种物品,我们需要计算$2^n-1$种情况,正常应用场景绝不可能才4种商品,这个时候就要提到Apriori原理,可以大大减少频繁项集的数目
Apriori原理:如果某个项集是频繁项集,那么它所有的子集也是频繁的.举个例子就是如果{0,1}是频繁的,那么{0},{1}也一定是频繁的,上面介绍过了,这里就不再细说了.正着看没什么用,但是反过来,即一个项集(例如{0},{1})是非频繁项集,则他的超集({0,1})也是非频繁的: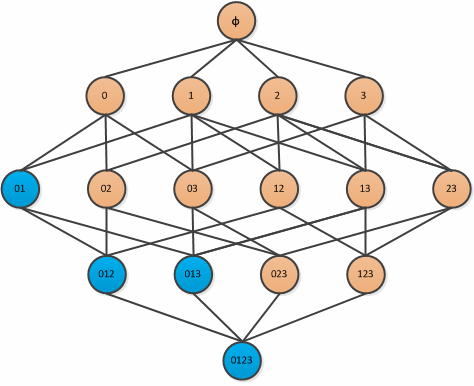
图中给出了所有可能的项集,其中蓝色表示非频繁项集,由于{0,1}非频繁,因此,它们的超集也是非频繁的,他们的支持度可以直接忽略,俗称减枝

使用Apriori返回目录

关联分析的两个目标:发现频繁项集和发现关联规则.首先要找到频繁项集,然后根据频繁项集找到关联规则.
Apriori寻找频繁项集的一般步骤是:

  1. 首先生成所有单个物品的项集列表
  2. 扫描交易记录查看哪些项集满足最小支持度要求,去掉那些不满足的项集
  3. 对剩下的项集进行组合生成包含两个元素的项集
  4. 重复2~3,直到所有项集都被去掉

下面看看Python代码实现:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
# -*- coding: utf-8 -*-

def loadDataSet():
    """
    创建一个用于测试的简单的数据集
    如果需要从其他地方加载产生数据,只需要重写这个方法即可
    """
    return [[1, 3, 4], [2, 3, 5], [1, 2, 3, 5], [2, 5]]

def createC1(dataSet):
    """
    构建初始候选项集(Candidate)的列表，即所有候选项集只包含一个元素，
    C1是大小为1的所有候选项集的集合
    """
    C1 = []
    for transaction in dataSet:
        for item in transaction:
            if [item] not in C1:
                C1.append([item])
    C1.sort()
    return map(frozenset, C1)

def scanD(D, Ck, minSupport):
    """
    计算Ck中的项集在数据集合D(记录或者transactions)中的支持度,
    返回满足最小支持度的项集的集合，和所有项集支持度信息的字典。
    """
    ssCnt = {}
    for tid in D:
        # 对于每一条transaction
        for can in Ck:
            # 对于每一个候选项集can，检查是否是transaction的一部分
            # 即该候选can是否得到transaction的支持
            if can.issubset(tid):
                if not ssCnt.has_key(can):
                    ssCnt[can] = 1
                else:
                    ssCnt[can] += 1
    numItems = float(len(D))
    retList = []
    supportData = {}
    for key in ssCnt:
        # 每个项集的支持度
        support = ssCnt[key] / numItems

        # 将满足最小支持度的项集，加入retList
        if support >= minSupport:
            retList.insert(0, key)

        # 汇总支持度数据
        supportData[key] = support
    return retList, supportData

上面代码中 “frozenset”，是为了冻结集合，使集合由“可变”变为 “不可变”，这样，这些集合就可以作为字典的键值.测试一下上面的代码:

1
2
3
4
5
6
7
8
9
10
11
12
13
if __name__ == '__main__':
    # 导入数据集
    myDat = loadDataSet()
    # 构建第一个候选项集列表C1
    C1 = createC1(myDat)

    # 构建集合表示的数据集 D
    D = map(set, myDat)
    # 选择出支持度不小于0.5 的项集作为频繁项集
    L, suppData = scanD(D, C1, 0.5)

    print u"频繁项集L：", L
    print u"所有候选项集的支持度信息：", suppData

看看运行出来的结果:

1
2
频繁项集L： [frozenset([1]), frozenset([3]), frozenset([2]), frozenset([5])]
所有候选项集的支持度信息： {frozenset([4]): 0.25, frozenset([5]): 0.75, frozenset([2]): 0.75, frozenset([3]): 0.75, frozenset([1]): 0.5}

可以看出，只有支持度不小于0.5的项集被选中到L中作为频繁项集，根据不同的需求，我们可以设定最小支持度的值，从而得到我们想要的频繁项集.
上面我们找出了只含有一个元素的频繁项集,下面需要整合一下代码,一次选择